Movimientos en el Plano (Transformaciones Isométricas)
Trabajaremos con Traslación, Reflexión, Rotación y Homotecia en el plano cartesiano.
Identificación del Grupo
Esta información se usará para nombrar sus evidencias fotográficas. **Por favor, ingrésala antes de comenzar a subir fotos.**
Conceptos Fundamentales
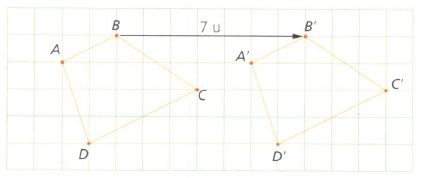
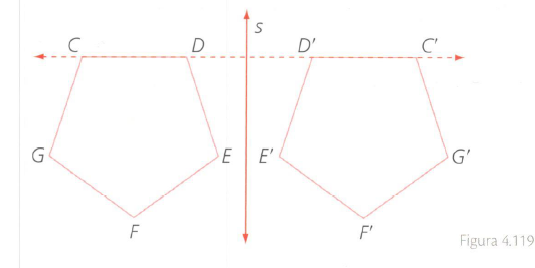
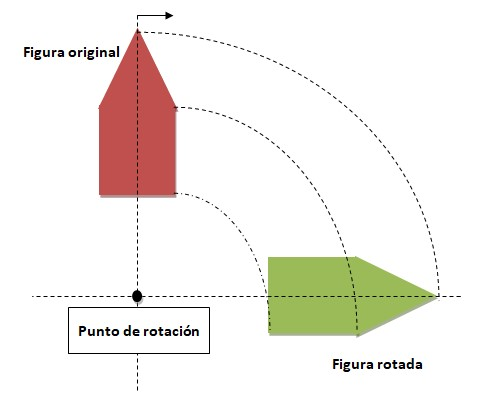
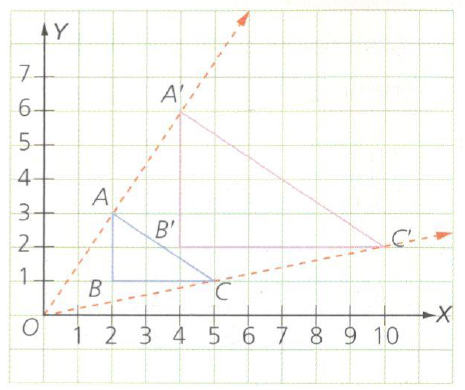
Las **Transformaciones Isométricas** (Traslación, Reflexión, Rotación) mantienen la forma y el tamaño de la figura original. La **Homotecia** sí cambia el tamaño, manteniendo la forma.
Tareas de Aplicación en el Plano Cartesiano 🗺️
Trabajen en papel milimetrado o en una cuadrícula. Dibujen la figura original y la figura transformada, usando un color diferente para cada una. **¡No olviden marcar el eje de reflexión, el centro de rotación/homotecia o el vector de traslación!**
1. Traslación: El Deslizamiento del Triángulo
A. Figura Original: Dibujen un triángulo con vértices $\mathbf{A(1, 2)}$, $\mathbf{B(4, 5)}$ y $\mathbf{C(6, 1)}$.
B. Traslación: Apliquen una traslación definida por el vector $\mathbf{\vec{v} = (-5, 3)}$.
Escriban los nuevos vértices $\mathbf{A'}$, $\mathbf{B'}$ y $\mathbf{C'}$ y el cálculo que usaron.
Pregunta de Reflexión y Razonamiento
1.1. **Composición de Vectores:** Si volvieran a aplicar la misma traslación $\mathbf{\vec{v} = (-5, 3)}$ a la figura resultante ($\mathbf{A'B'C'}$), ¿cuál sería el único vector de traslación que transformaría la figura original ($\mathbf{ABC}$) en la figura final ($\mathbf{A''B''C''}$)?
2. Reflexión: El Espejo del Cuadrilátero
A. Figura Original: Dibujen un cuadrilátero con vértices $\mathbf{P(-6, 4)}$, $\mathbf{Q(-3, 7)}$, $\mathbf{R(-1, 5)}$ y $\mathbf{S(-4, 2)}$.
B. Reflexión: Apliquen una reflexión con respecto al **eje Y** (la línea $\mathbf{x=0}$).
Escriban los nuevos vértices $\mathbf{P'}$, $\mathbf{Q'}$, $\mathbf{R'}$ y $\mathbf{S'}$ y expliquen la regla de transformación aplicada.
Pregunta de Reflexión y Razonamiento
2.1. **Interpretación del Eje:** Si en lugar de reflejar respecto al eje $\mathbf{Y\ (x=0)}$, la reflexión se hiciera sobre la línea vertical $\mathbf{x=-1}$, ¿cómo cambiarían las coordenadas del punto $\mathbf{P(-6, 4)}$ resultante? Justifiquen la diferencia en la coordenada $x$.
3. Rotación: El Giro del Polígono en L
A. Figura Original: Dibujen un polígono en forma de 'L' con vértices $\mathbf{A(1, 1)}$, $\mathbf{B(4, 1)}$, $\mathbf{C(4, 2)}$, $\mathbf{D(2, 2)}$, $\mathbf{E(2, 4)}$ y $\mathbf{F(1, 4)}$.
B. Rotación: Apliquen una rotación de $\mathbf{90^\circ}$ en sentido **antihorario** con centro de rotación en el $\mathbf{Origen\ (0, 0)}$.
Escriban los nuevos vértices $\mathbf{A'}$ a $\mathbf{F'}$ y la regla de transformación: $\mathbf{(x, y) \to (-y, x)}$
Pregunta de Reflexión y Razonamiento
3.1. **Análisis de Orientación:** ¿La rotación de $90^\circ$ antihorario en el origen cambia la orientación (el sentido en que se recorren los vértices) del polígono? ¿Por qué se dice que la Rotación es una **Isometría directa**?
4. Homotecia: La Ampliación y Reducción del Pentágono
A. Figura Original: Dibujen un pentágono con vértices $\mathbf{J(2, 1)}$, $\mathbf{K(4, 1)}$, $\mathbf{L(5, 3)}$, $\mathbf{M(3, 5)}$ y $\mathbf{N(1, 3)}$.
B. Homotecia de Ampliación: Apliquen una homotecia con centro de homotecia en el $\mathbf{Origen\ (0, 0)}$ y un factor de razón $k_1 = \mathbf{3}$.
C. Homotecia de Reducción: A la figura original, aplíquenle una segunda homotecia con centro $\mathbf{(0, 0)}$ y un factor de razón $k_2 = \mathbf{0.5}$.
Escriban los nuevos vértices $\mathbf{J'_1, K'_1, \dots}$ y $\mathbf{J'_2, K'_2, \dots}$ para cada caso. Expliquen el efecto de $k_1 > 1$ y $0 < k_2 < 1$ en el tamaño de la figura.
Preguntas de Reflexión y Razonamiento
4.1. **Diferencia Conceptual:** Si la homotecia con razón $k=1$ preserva la forma y el tamaño, ¿por qué la homotecia en general (con $k \neq 1$) **no** se clasifica como una **isometría**? Respondan en términos de la preservación de distancias.
4.2. **Relación de Magnitudes:** Si el perímetro del pentágono original es $P$, ¿cuál sería el perímetro del pentágono transformado por la Homotecia con factor $k_1=3$ ($\mathbf{P'}$)? ¿Qué relación existe entre $P'$ y $P$?
V. Tarea de Pixel Art: Combinación de Movimientos
Utilicen una cuadrícula grande (como 10x10) para desarrollar un diseño simple de **Pixel Art**. Tienes libertad creativa, pero aquí hay algunas ideas:

5. Pixel Art y Transformaciones Compuestas
A. Dibujo Original: Creen su dibujo de Pixel Art en el primer cuadrante. Identifiquen las coordenadas de **cuatro puntos clave** de su diseño (P1, P2, P3, P4).
B. Movimiento 1 (Reflexión): Reflejen su dibujo (la pre-imagen) con respecto al **eje X** (la línea $\mathbf{y=0}$).
C. Movimiento 2 (Traslación): A la figura resultante del paso B (la imagen 1), aplíquenle una traslación con el vector $\mathbf{\vec{v} = (8, 0)}$.
D. Resultado Final: El dibujo original, el reflejado y el trasladado deben verse en el mismo plano cartesiano.
Muestren las coordenadas finales de sus cuatro puntos clave después del Movimiento 1 y el Movimiento 2.
Pregunta de Reflexión y Razonamiento
5.1. **Conmutatividad de Movimientos:** Si invirtieran el orden de las transformaciones (primero la Traslación $\mathbf{\vec{v}=(8, 0)}$ y luego la Reflexión sobre el eje $\mathbf{X}$), ¿el dibujo final quedaría en la misma posición? Justifiquen su respuesta utilizando las coordenadas finales de uno de los puntos clave para ambos órdenes.
Sube las fotos de tu dibujo a mano y las coordenadas finales escritas.
VI. Conclusión y Coordenadas Finales
Asegúrate de haber completado las 5 tareas y subido todas las evidencias. Responde esta pregunta final en tu cuaderno y sube la foto de la respuesta.
Pregunta de Síntesis
¿Qué diferencia fundamental hay entre el resultado final de la **Traslación** y la **Rotación** comparado con el de la **Homotecia**? Usa el concepto de **isometría** en tu respuesta y explica qué magnitud se conserva en un caso y en el otro no.